Geometric Mean(GM)

 Geometric Mean(GM)

(a) G.M. For Ungrouped data

The Geometric Mean (G.M.) of a set of n observations is the nth root of their product. If x1, x2, ... , xn are n observations then

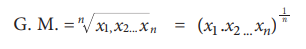
Taking the nth root of a number is difficult. Thus, the computation is done as under

Example 1

Calculate the geometric mean of the annual percentage growth rate of profits in business corporate from the year 2000 to 2005 is given below

50, 72, 54, 82, 93

Solution:

Example 2

The population in a city increased at the rate of 15% and 25% for two successive years. In the next year it decreased at the rate of 5%. Find the average rate of growth

Solution:

Let us assume that the population is 100

(b) G.M. For Discrete grouped data

If x1, x2,……xn are discrete values of the variate x with corresponding frequencies f1, f2, ... fn. Then geometric mean is defined as

Example 3

Find the G.M for the following data, which gives the defective screws obtained in a factory.

Solution:

(c) G.M. for Continuous grouped data

Example 4

The following is the distribution of marks obtained by 109 students in a subject in an institution. Find the Geometric mean.

Solution:

Geometric Mean(GM) video link ;